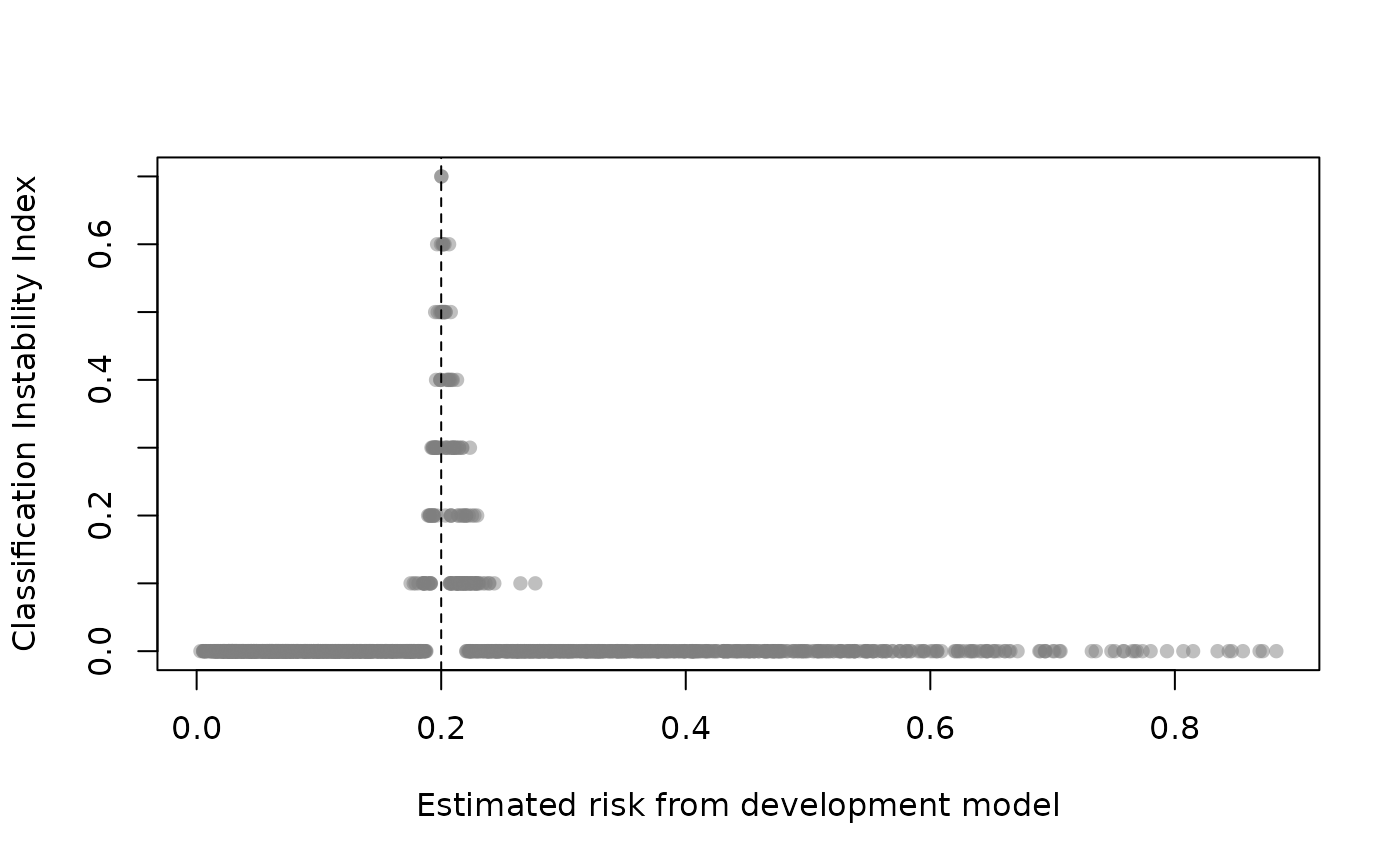
Classification instability plot

Classification instability plot shows the relationship between original model estimated risk and the classification instability index (CII). The CII is the proportion of bootstrap replicates where the predicted class (0 if p <= threshold; 1 if p > threshold) is different to that obtained from the original model. Those with risk predictions around the threshold will exhibit elevated CII but an unstable model will exhibit high CII across a range of risk predictions. See Riley and Collins (2023).

Usage

classification_stability(
  x,
  threshold,
  xlim,
  ylim,
  xlab,
  ylab,
  pch,
  cex,
  col,
  subset,
  plot = TRUE
)

Arguments

x

an object produced by validate with method = "boot_*" (or boot_optimism with method="boot")

threshold

estimated risks above the threshold get a predicted 'class' of 1, otherwise 0.

xlim

x limits (default = range of estimated risks)

ylim

y limits (default = c(0, maximum CII))

xlab

a title for the x axis

ylab

a title for the y axis

pch

plotting character (default = 16)

cex

controls point size (default = 1)

col

color of points (default = grDevices::grey(.5, .5))

subset

vector of observations to include (row indices). This can be used to select a random subset of observations.

plot

if FALSE just returns CII values (see value)

Value

plots classification (in)stability. Invisibly returns estimates of CII for each observation.

References

Riley, R. D., & Collins, G. S. (2023). Stability of clinical prediction models developed using statistical or machine learning methods. Biometrical Journal, 65(8), 2200302. doi:10.1002/bimj.202200302

Examples

set.seed(456)
# simulate data with two predictors that interact
dat <- pmcalibration::sim_dat(N = 2000, a1 = -2, a3 = -.3)
mean(dat$y)
#> [1] 0.1985
dat$LP <- NULL # remove linear predictor

# fit a (misspecified) logistic regression model
m1 <- glm(y ~ ., data=dat, family="binomial")

# internal validation of m1 via bootstrap optimism with 10 resamples
# B = 10 for example but should be >= 200 in practice
m1_iv <- validate(m1, method="boot_optimism", B=10)
#> It is recommended that B >= 200 for bootstrap validation

classification_stability(m1_iv, threshold=.2)