Skip to contents

Create a calibration curve

Source: R/pmcalibration.R
pmcalibration.Rd

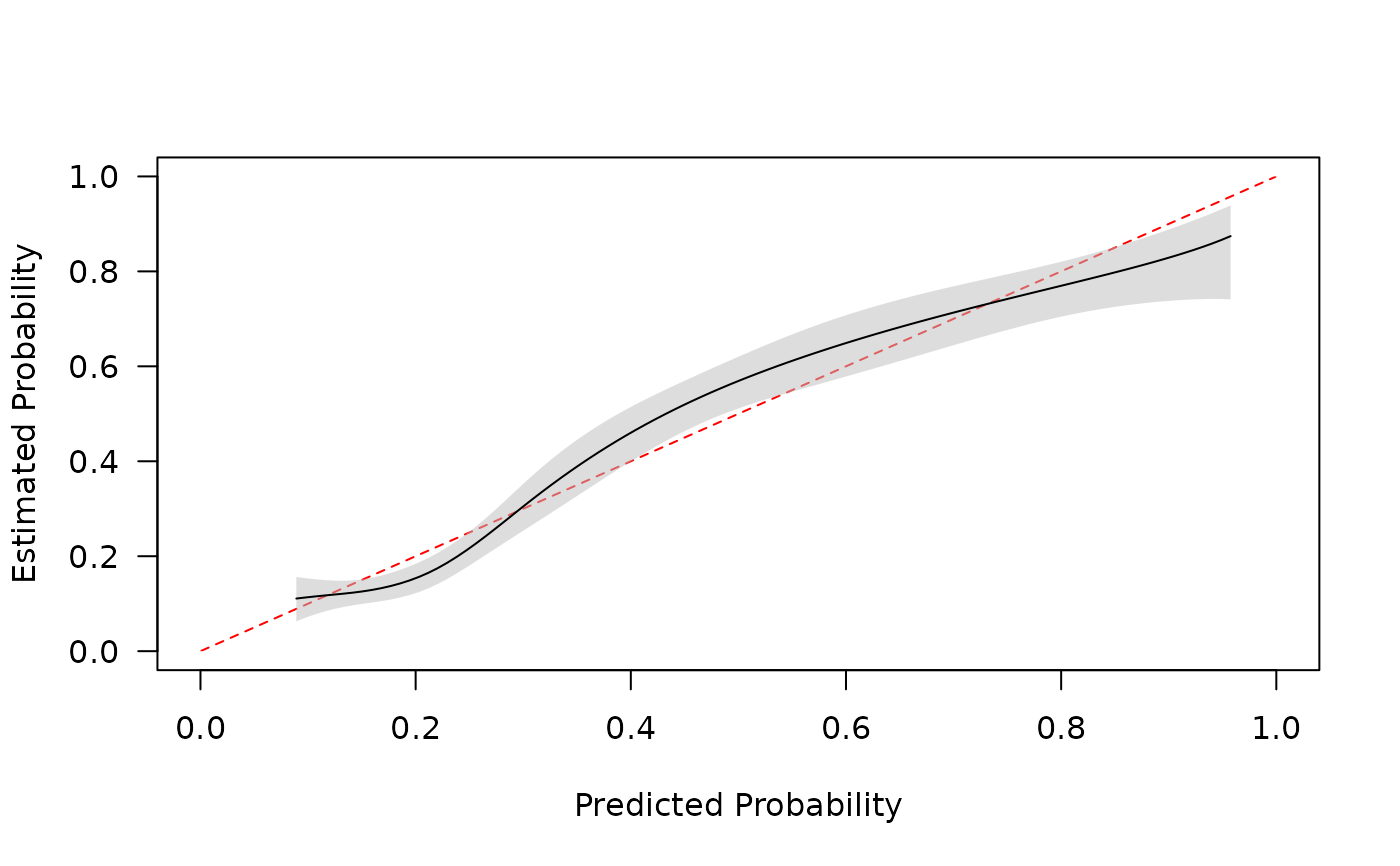
Assess calibration of clinical prediction models (agreement between predicted and observed probabilities) via different smooths. Binary and time-to-event outcomes are supported.

Usage

pmcalibration(
  y,
  p,
  smooth = c("gam", "none", "ns", "bs", "rcs", "lowess", "loess"),
  time = NULL,
  ci = c("sim", "boot", "pw", "none"),
  n = 1000,
  transf = NULL,
  eval = 100,
  plot = TRUE,
  ...
)

Arguments

y

a binary or a right-censored time-to-event outcome. Latter must be an object created via survival::Surv.

p

predicted probabilities from a clinical prediction model. For a time-to-event object time must be specified and p are predicted probabilities of the outcome happening by time units of time follow-up.

smooth

what smooth to use. Available options:

  • 'gam' (default) = generalized additive model via mgcv::gam and mgcv::s. Optional arguments are bs, k, fx, method (see ?mgcv::gam and ?mgcv::s)

  • 'rcs' = restricted cubic spline using rms::rcs. Optional arguments for this smooth are nk (number of knots; defaults to 5) and knots (knot positions; set by Hmisc::rcs.eval if not specified)

  • 'ns' = natural spline using splines::ns. Optional arguments are df (default = 6), knots, Boundary.knots (see ?splines::ns)

  • 'bs' = B-spline using splines::bs. Optional arguments are df (default = 6), knots, Boundary.knots (see ?splines::bs)

  • 'lowess' = uses lowess(x, y, iter = 0) based on rms::calibrate. Only for binary outcomes.

  • 'loess' = uses loess with all defaults. Only for binary outcomes.

  • 'none' = logistic or Cox regression with single predictor variable (for binary outcome performs logistic calibration when transf = "logit"). See logistic_cal

'rcs', 'ns', 'bs', and 'none' are fit via glm or survival::coxph and 'gam' is fit via mgcv::gam with family = Binomial(link="logit") for a binary outcome or mgcv::cox.ph when y is time-to-event.

time

what follow up time do the predicted probabilities correspond to? Only used if y is a Surv object

ci

what kind of confidence intervals to compute?

  • 'sim' = simulation based inference. Note this is currently only available for binary outcomes. n samples are taken from a multivariate normal distribution with mean vector = coef(mod) and variance covariance = vcov(model).

  • 'boot' = bootstrap resampling with n replicates. y and p are sampled with replacement and the calibration curve is reestimated. If knots are specified the same knots are used for each resample (otherwise they are calculated using resampled p or transformation thereof)

  • 'pw' = pointwise confidence intervals calculated via the standard errors produced by relevant predict methods. Only for plotting curves; if selected, CIs are not produced for metrics (not available for smooth = 'lowess')

Calibration metrics are calculated using each simulation or boot sample. For both options percentile confidence intervals are returned.

n

number of simulations or bootstrap resamples

transf

transformation to be applied to p prior to fitting calibration curve. Valid options are 'logit', 'cloglog', 'none', or a function (must retain order of p). If unspecified defaults to 'logit' for binary outcomes and 'cloglog' (complementary log-log) for time-to-event outcomes.

eval

number of points (equally spaced between min(p) and max(p)) to evaluate for plotting (0 or NULL = no plotting). Can be a vector of probabilities.

plot

should a plot be produced? Default = TRUE. Plot is created with default settings. See plot.pmcalibration.

...

additional arguments for particular smooths. For ci = 'boot' the user is able to run samples in parallel (using the parallel package) by specifying a cores argument

Value

a pmcalibration object containing calibration metrics and values for plotting

References

Austin P. C., Steyerberg E. W. (2019) The Integrated Calibration Index (ICI) and related metrics for quantifying the calibration of logistic regression models. Statistics in Medicine. 38, pp. 1–15. https://doi.org/10.1002/sim.8281

Van Calster, B., Nieboer, D., Vergouwe, Y., De Cock, B., Pencina M., Steyerberg E.W. (2016). A calibration hierarchy for risk models was defined: from utopia to empirical data. Journal of Clinical Epidemiology, 74, pp. 167-176. https://doi.org/10.1016/j.jclinepi.2015.12.005

Austin, P. C., Harrell Jr, F. E., & van Klaveren, D. (2020). Graphical calibration curves and the integrated calibration index (ICI) for survival models. Statistics in Medicine, 39(21), 2714-2742. https://doi.org/10.1002/sim.8570

Examples

# binary outcome -------------------------------------
library(pmcalibration)
# simulate some data
n <- 500
dat <- sim_dat(N = n, a1 = .5, a3 = .2)
head(dat)
#>            x1          x2 y         LP
#> 1 -0.79656573  0.78782032 1 0.36574445
#> 2  0.99246366  2.17238436 1 4.09605053
#> 3 -0.32348141  2.49976601 1 2.51455903
#> 4  0.04091126 -0.43830184 1 0.09902312
#> 5 -0.08776347  0.49726921 1 0.90077732
#> 6 -0.21569343  0.09228747 0 0.37261288
# predictions
p <- with(dat, invlogit(.5 + x1 + x2 + x1*x2*.1))

# fit calibration curve
cal <- pmcalibration(y = dat$y, p = p, smooth = "gam", k = 20, ci = "pw")


summary(cal)
#> Calibration metrics based on a calibration curve estimated for a binary outcome via a generalized additive model (see ?mgcv::s) using logit transformed predicted probabilities.
#> 
#>      Estimate
#> Eavg    0.021
#> E50     0.015
#> E90     0.044
#> Emax    0.046
#> ECI     0.065

plot(cal)

# time to event outcome -------------------------------------
library(pmcalibration)
if (requireNamespace("survival", quietly = TRUE)){
library(survival)

data('transplant', package="survival")
transplant <- na.omit(transplant)
transplant = subset(transplant, futime > 0)
transplant$ltx <- as.numeric(transplant$event == "ltx")

# get predictions from coxph model at time = 100
# note that as we are fitting and evaluating the model on the same data
cph <- coxph(Surv(futime, ltx) ~ age + sex + abo + year, data = transplant)

time <- 100
newd <- transplant; newd$futime <- time; newd$ltx <- 1
p <- 1 - exp(-predict(cph, type = "expected", newdata=newd))
y <- with(transplant, Surv(futime, ltx))

cal <- pmcalibration(y = y, p = p, smooth = "rcs", nk=5, ci = "pw", time = time)

summary(cal)

plot(cal)

}